Eva y sus apuntes

Se trata de un estándar para representar números en coma flotante para que sea igual en un procesador que en otro. El IEEE 754 tiene una representación para 32 bit y otra para 64 bit. La representación de 32 bit cuenta con: Un bit para el signo 8 bits para el exponente 23 bits para la mantisa La representación de 64 bit cuenta con: Un bit para el signo 11 bits para el exponente 52 bits para la mantisa Nosotros nos vamos a centrar en el de 32 bit. Su estructura es: + 0'1bbb...b·2 Exponente S: Signo El signo puede ser positivo (+) o negativo (-), en binario vamos a representar al positivo con un 0 y al negativo con un 1. Como todos los números que vamos a representar con IEEE 754 tienen que empezar con 0'1bbb...·2 Exponente , a ese 1 le vamos a llamar "bit implícito". La mantisa van a ser todas esas "b", omitiendo al bit implícito. Se omite al bit implícito a la hora de representarlo en nuestra estructura de IEEE-754 para poder repr

Los circuitos están realizados con logic.ly  por si queréis probarlos, es una demo online que se puede abrir en el navegador de Internet de cualquier sistema operativo. Sumador Empecemos con el half-adder y despúes con el Full-adder. (La diferencia entre ellos es que en uno ya puedes sumar llevando) Half-adder Tabla de verdad S es resultado de la suma binaria, y C es el carry (la que te llevas) Circuito Full-adder Tabla de verdad Cin es la que te llevas, en el circuito hay que encencer Cin de forma manual para así poder verlo con más calma. Circuito Restadores Al igual que con la suma existe el half-subtractor y el full-subtractor. Half-Subtractor Tabla Circuito Full-subtractor Tabla Circuito Tanto al sumador como al restador los podemos hacer tan grandes como nosotros consideremos competente, estos ejemplos están realizados con la suma/resta de un bit, pero se puede hacer con los bits que nosotros queramos, tan solo tendríamos qu

Esto va como continuación de la entrada NAND y NOR puertas universales Este es un ejemplo para ver que sí que se puede construir cualquier circuito con estas puertas (puesto que ya hice en la otra entrada AND, OR y NOT). Puerta XOR Esta puerta solo deja corriente cuando A y B son distintos entre sí. El circuito con puertas NAND sería: El circuito con puertas NOR sería:

Estas puertas lógicas son consideradas universales al poder crear un circuito equivalente a las puertas OR, AND o NOT utilizando puertan NAND o solo con puertas NOR. Voy a mostraros como serían los circuitos con las puertas NOR y NAND de las puertas OR, AND y NOT. (Los circuitos están realizados con logic.ly ) Puertas NAND NOT AND OR Puertas NOR NOT Puerta AND Puerta OR

Puertas Lógicas Puerta Not Tabla de verdad Puerta AND Puerta OR Puerta NAND Puerta NOR Puerta XOR Para poner estos conocimientos a prueba de una forma más dinámica os recomiendo la App "Make It True"

Minterm:  Producto lógico de todas las variables negadas o sin negar (producto canónico). Maxterm : Suma lógica de todas las variables negadas o sin negar (suma canónica). Tabla: a b c   Minterms   Maxterms 0 0 0   m 0 =a c ·b c ·c c   M 0 =a+b+c 0 0 1   m 1 =a c ·b c ·c   M 1 =a+b+c c 0 1 0   m 2 =a c ·b·c c   M 2 =a+b c +c 0 1 1   m 3 =a c ·b·c   M 3 =a+b c +c c 1 0 0   m 4 =a·b c ·c c   M 4 =a c +b+c 1 0 1   m 5 =a·b c ·c   M 5 =a c +b+c c 1 1 0   m 6 =a·b·c c   M 6 =a c +b c +c 1 1 1   m 7 =a·b·c   M 7 =a c +b c +c c Para pasar de miniterms a Maxterms hay que negar 2 veces la función. Los minterms se utilizan para los mapas de Karnaugh. Mapas de Karnaugh   Los mapas de Karnaugh sirven para simplificar funciones booleanas. Por ejemplo: vamos a simplificar: f(a,b,c,d)=a c b c c c d c +a c bc c d c +a c b c c c d+a c bc c d+abc c d c +abcd c Vamos a crear nuestra tabla de verdad con los datos que

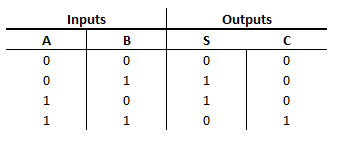
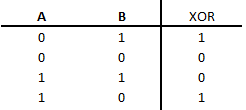
Álgebra de Boole x y z f(x,y,z) 0 0 0 f(0,0,0) 0 0 1 f(0,0,1) 0 1 0 f(0,1,0) 0 1 1 f(0,1,1) 1 0 0 f(1,0,0) 1 0 1 f(1,0,1) 1 1 0 f(1,1,0) 1 1 1 f(1,1,1) Teorema de expansión de Shannon f(x 1 ,x 2 ,...,x n ) x i € {0,1} f: {0,1} n ->{0,1}                                               _ f(x 1 ,x 2 ,...,x n ) = x 1 ·f(1,x 2 ,...x n )+ x 1 · f(0,x 1 ,...,x n ) Por ejemplo, el teorema de expansión de Shannon aplicado a f(x,y,z) sería: f(x,y,z)=xf(1,y,z)+x*f(0,y,z)=xyf(1,1,z) + xy*f(1,0,z) + x*yf(0,1,z) + x*y*f(0,0,z)= =xyzf(1,1,1) + xyz*f(1,1,0) + xy*zf(1,0,1) + xy*z*f(1,0,0) + x*yzf(0,1,1) + x*yz*f(0,1,0) + x*y*zf(0,0,1) + x*y*z*f(0,0,0)

P tiene impurezas aceptoras N tiene impurezas donoras Al recombinarse, P queda cargado negativamente, y N queda cargado positivamente. Aparece un campo eléctrico que se va a oponer al paso de los huecos hacia el lado N, y a lo electrones hacia P. En la línea del centro de la imagen se muestra el equilibrio dinámico alcanzado, denominado región de carga espacial o región de agotamiento. Si lo conectamos a una diferencia de potencial hay varios casos: Que no haya diferencia de potencial (V=0), encontramos la región de agotamiento como en la primera imagen. Que exista una diferencia de potencial superior en la entrada de P que en la de N (positivo con positivo, negativo con negativo), la región de carga espacial disminuye al aumentar el número de portadores. Aparece una corriente eléctrica. Que exista una diferencia de potencial inferior en la entrada de P que en la de N (negativo a p, n con positivo). En este caso la región de agotamiento aumenta. Se denomina polarización e

La capa superior es el nivel de energía de conducción. (E C ) La capa inferior es el nivel de energía de valencia. (E V ) La diferencia que existe entre ambos niveles se llama energía del "gap" (E g ), que es el mínimo de energía que hay que añadir para liberar a un electrón. 1 eV=1'6·10 -19 J Según sea el material, esta energía será mayor o menor: No existe en los conductores Es pequeña en los semiconductores (2 eV aproximadamente) Es más grande en los aislantes La energía del nivel de Fermi (E F )es el mínimo de energía que hay que suministrar para que los electrones menos ligados (suministrados por las impurezas Donoras o pentavalentes) para que salte a la banda de conducción. El material está muy dopado si E C - E F = 0 Para calcular a n y p: En el caso del Puro: Ahora que ya tenemos al caso puro, vamos a calcular el Nivel de Fermi de un semiconductor puro.

La carga positiva total es igual que la carga negativa total porque el material (el semiconductor) es neutro. Q + =Q - Silicio: átomos/cm 3 ~10 22 cm -3 Silicio con impurezas de fósforo Si añadimos impurezas de P (fósforo) en la relación: 1 átomo de P ~10.000 átomos Si Nos quedan 10 18 átomos de P/ cm 3 y 10 22 átomo de Si/cm 3 a 0 Kelvin. A temperatura ambiente tendremos: 10 18 electrones/cm 3 del P 10 10 electrones/cm 3 del Si Pasaría algo similar si hubiéramos añadido un elemento trivalente, pero con huecos. A estos materiales que al añadirlos al Silicio proporcionan un electrón por cada átomo se le llaman impurezas donoras . A los materiales que al añadirlos al Silicio proporcionan un hueco por cada átomo se le llaman impurezas aceptoras . Estas impurezas son ionizadas con mucha más facilidad. Q + = p + N d + a T=Temperatura Ambiente. (Donoras) Q - = n + N a - a T=Temperatura Ambiente. (Aceptoras) Q + =Q - n+N a =p+N d (A temperatura ambien

El carbono genera enlaces muy estables al tener 4 electrones en su capa más externa. Sin el carbono no existiría la vida en la Tierra tal como la conocemos. El silicio es otro elemento que también genera enlaces muy estables, y es un elemento muy presente en la Tierra, que forma estructuras cristalinas, y, que además de conducir bastante bien la electricidad, su conductividad puede ser controlada. Al controlar el número de portadores , se controla el número de electrones que se pueden mover. En 1 cm 3  hay aproximadamente en el orden de 10 22 electrones. Los átomos del silicio forman enlaces covalentes con otros átomos de silicio de forma que no queda ningún electrón libre. Si se rompe la figura cristalina se pueden observar que los electrones de la zona de ruptura (en la superficie) están en movimiento. Si colocáramos al material a temperatura 0 Kelvin (0 absoluto) los átomos estarían quietos, y a medida que vamos aumentando la temperatura los electrones se van colisionand

Fase 1: Resolución del problema. Algoritmo Análisis del problema: Comprensión y definición del problema Solución General (Algoritmo): desarrollo de una secuencia lógica de pasos usados para resolver el problema. Verificación y prueba: Seguir los pasos exactos -tal y como se han descrito- para comprobar que se resuelve el problema. Fase 2: Implementación del algoritmo. Programa Solución específica (Programa): Traducción del algoritmo a un lenguaje de programación Prueba: Hacer que la computadora siga las instrucciones Uso Fase 3: Codificación Escribir el algoritmo en forma de programa. Fase 4: Depuración Detección y corrección de errores.

Este blog ha sido creado para compartir apuntes y todos los comentarios que ayuden a la ampliación de conocimientos por parte de los usuarios de Internet serán tremendamente agradecidos ^_^.