Minterms y Maxterms
Minterm: Producto lógico de todas las variables negadas o sin negar (producto canónico).
Maxterm: Suma lógica de todas las variables negadas o sin negar (suma canónica).
Tabla:
Para pasar de miniterms a Maxterms hay que negar 2 veces la función.
Los minterms se utilizan para los mapas de Karnaugh.


Los mapas de Karnaugh sirven para simplificar funciones booleanas.
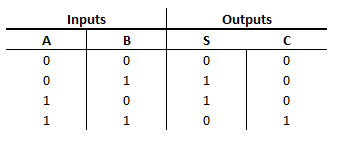
Por ejemplo: vamos a simplificar: f(a,b,c,d)=acbcccdc+acbccdc+acbcccd+acbccd+abccdc+abcdc
Vamos a crear nuestra tabla de verdad con los datos que tenemos:

Ahora los introducimos en nuestro mapa de karnaugh
Y lo simplificamos haciendo grupos de potencias de dos

Y el resultado es:accc + abdc esto se logra dejando de los grupos las variables que no varían y "quitando" las que sí. Por ejemplo, en el grupo de dos tanto a como b se mantienen constantes, al igual que la d negada, mientras que c varía, obteniendo el segundo sumando.
Maxterm: Suma lógica de todas las variables negadas o sin negar (suma canónica).
Tabla:
| a | b | c | Minterms | Maxterms |
| 0 | 0 | 0 | m0=ac·bc·cc | M0=a+b+c |
| 0 | 0 | 1 | m1=ac·bc·c | M1=a+b+cc |
| 0 | 1 | 0 | m2=ac·b·cc | M2=a+bc+c |
| 0 | 1 | 1 | m3=ac·b·c | M3=a+bc+cc |
| 1 | 0 | 0 | m4=a·bc·cc | M4=ac+b+c |
| 1 | 0 | 1 | m5=a·bc·c | M5=ac+b+cc |
| 1 | 1 | 0 | m6=a·b·cc | M6=ac+bc+c |
| 1 | 1 | 1 | m7=a·b·c | M7=ac+bc+cc |
Para pasar de miniterms a Maxterms hay que negar 2 veces la función.
Los minterms se utilizan para los mapas de Karnaugh.
Mapas de Karnaugh


Los mapas de Karnaugh sirven para simplificar funciones booleanas.
Por ejemplo: vamos a simplificar: f(a,b,c,d)=acbcccdc+acbccdc+acbcccd+acbccd+abccdc+abcdc

Ahora los introducimos en nuestro mapa de karnaugh
Y lo simplificamos haciendo grupos de potencias de dos

Y el resultado es:accc + abdc esto se logra dejando de los grupos las variables que no varían y "quitando" las que sí. Por ejemplo, en el grupo de dos tanto a como b se mantienen constantes, al igual que la d negada, mientras que c varía, obteniendo el segundo sumando.



Comentarios
Publicar un comentario