Eva y sus apuntes

Se trata de un estándar para representar números en coma flotante para que sea igual en un procesador que en otro. El IEEE 754 tiene una representación para 32 bit y otra para 64 bit. La representación de 32 bit cuenta con: Un bit para el signo 8 bits para el exponente 23 bits para la mantisa La representación de 64 bit cuenta con: Un bit para el signo 11 bits para el exponente 52 bits para la mantisa Nosotros nos vamos a centrar en el de 32 bit. Su estructura es: + 0'1bbb...b·2 Exponente S: Signo El signo puede ser positivo (+) o negativo (-), en binario vamos a representar al positivo con un 0 y al negativo con un 1. Como todos los números que vamos a representar con IEEE 754 tienen que empezar con 0'1bbb...·2 Exponente , a ese 1 le vamos a llamar "bit implícito". La mantisa van a ser todas esas "b", omitiendo al bit implícito. Se omite al bit implícito a la hora de representarlo en nuestra estructura de IEEE-754 para poder repr...

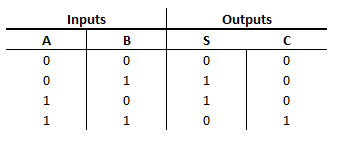
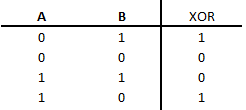
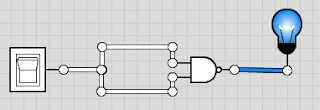
Los circuitos están realizados con logic.ly  por si queréis probarlos, es una demo online que se puede abrir en el navegador de Internet de cualquier sistema operativo. Sumador Empecemos con el half-adder y despúes con el Full-adder. (La diferencia entre ellos es que en uno ya puedes sumar llevando) Half-adder Tabla de verdad S es resultado de la suma binaria, y C es el carry (la que te llevas) Circuito Full-adder Tabla de verdad Cin es la que te llevas, en el circuito hay que encencer Cin de forma manual para así poder verlo con más calma. Circuito Restadores Al igual que con la suma existe el half-subtractor y el full-subtractor. Half-Subtractor Tabla Circuito Full-subtractor Tabla Circuito Tanto al sumador como al restador los podemos hacer tan grandes como nosotros consideremos competente, estos ejemplos están realizados con la suma/resta de un bit, pero se puede hacer con los bits que nosotros queramos, tan solo...

Esto va como continuación de la entrada NAND y NOR puertas universales Este es un ejemplo para ver que sí que se puede construir cualquier circuito con estas puertas (puesto que ya hice en la otra entrada AND, OR y NOT). Puerta XOR Esta puerta solo deja corriente cuando A y B son distintos entre sí. El circuito con puertas NAND sería: El circuito con puertas NOR sería:

Estas puertas lógicas son consideradas universales al poder crear un circuito equivalente a las puertas OR, AND o NOT utilizando puertan NAND o solo con puertas NOR. Voy a mostraros como serían los circuitos con las puertas NOR y NAND de las puertas OR, AND y NOT. (Los circuitos están realizados con logic.ly ) Puertas NAND NOT AND OR Puertas NOR NOT Puerta AND Puerta OR

Puertas Lógicas Puerta Not Tabla de verdad Puerta AND Puerta OR Puerta NAND Puerta NOR Puerta XOR Para poner estos conocimientos a prueba de una forma más dinámica os recomiendo la App "Make It True"

Minterm:  Producto lógico de todas las variables negadas o sin negar (producto canónico). Maxterm : Suma lógica de todas las variables negadas o sin negar (suma canónica). Tabla: a b c   Minterms   Maxterms 0 0 0   m 0 =a c ·b c ·c c   M 0 =a+b+c 0 0 1   m 1 =a c ·b c ·c   M 1 =a+b+c c 0 1 0   m 2 =a c ·b·c c   M 2 =a+b c +c 0 1 1   m 3 =a c ·b·c   M 3 =a+b c +c c 1 0 0   m 4 =a·b c ·c c   M 4 =a c +b+c 1 0 1   m 5 =a·b c ·c   M 5 =a c +b+c c 1 1 0   m 6 =a·b·c c   M 6 =a c +b c +c 1 1 1   m 7 =a·b·c   M 7 =a c +b c +c c Para pasar de miniterms a Maxterms hay que negar 2 veces la función. Los minterms se utilizan para los mapas de Karnaugh. Mapas de Karnaugh   Los mapas de Karnaugh sirven para simplificar funciones booleanas. Por ejemplo: vamos a simplificar: f(a,b,c,d)=a c b c c c d c +a c bc c d c +a c ...